Chi-Square Test

Definition: The Chi-Square Test is the widely used non-parametric statistical test that describes the magnitude of discrepancy between the observed data and the data expected to be obtained with a specific hypothesis.

The observed and expected frequencies are said to be completely coinciding when the χ² = 0 and as the value of χ² increases the discrepancy between the observed and expected data becomes significant. The following formula is used to calculate Chi-square:

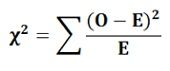Where,
O = Observed Frequency
E = Expected or Theoretical Frequency

The computed value of χ² is compared with the table value of χ² for a given degree of freedom and at a given significance level. If the calculated value exceeds the table value, then the difference between the observed frequencies and expected frequencies is said to be significant, i.e. it could not have arisen due to the fluctuations in simple sampling.

On the other hand, if the computed value is less than the table value, then the difference between the observed frequencies and expected frequencies is considered insignificant, i.e. might have been occurred due to the fluctuations in simple sampling.

The following five basic conditions should be met before applying the chi-square test:

1. The observation data must be independent of each other.
2. The data should be expressed in original units and not in percentage or ratio form so that it can be easily compared.
3. The data must be drawn randomly from the target population.
4. The sample should include at least 50 observations.
5. Every cell must have five or more observations. Each data entry is called a cell. In case, the observations are less than 5, then the value of χ² shall be overestimated and will result in the rejection of several Null Hypothesis.

Thus, the chi-Square test is one of the simplest non-parametric tests in statistical work where no assumption about the population being sampled is made.