Definition: The Fixed Proportion Production Function, also known as a Leontief Production Function implies that fixed factors of production such as land, labor, raw materials are used to produce a fixed quantity of an output and these production factors cannot be substituted for the other factors.
In other words, fixed quantity of inputs is used to produce the fixed quantity of output. All the factors of production are fixed and cannot be substituted for one another. Suppose there are 50 workers required to produce 500 units of a product, then the technical Coefficient of production will be 1/10. In the case of a fixed proportion production function, this one tenth of labor must be employed for the production of fixed output and no other factors of production can be substituted in place of labor.
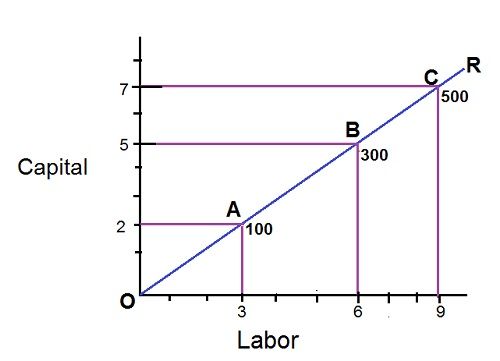
The concept of fixed proportion production function can be further understood with the help of a figure as shown below:
In the given figure, OR shows the fixed labor-capital ratio, if a firm wants to produce 100 units of a product, then 2 units of capital and 3 units of labor must be employed to attain this output.
Similarly, for the production of 300 and 500 units of a product, 5 units of capital and 6 units of labor and 7 units of capital and 9 units of labor must be employed respectively.
It may be noticed that along the isoquant curve the marginal product of a factor is zero, lets say, for the production of 300 units of a product, the capital is fixed (say 5 units), then any additional units of a labor won’t make any difference in the total production, hence, the marginal product of labor is zero.

abhi says
thnx for your help
sasmita says
Thanx to improve our study