Ordinal Approach to Consumer Equilibrium

Definition: The Ordinal Approach to Consumer Equilibrium asserts that the consumer is said to have attained equilibrium when he maximizes his total utility (satisfaction) for the given level of his income and the existing prices of goods and services. The ordinal approach defines two conditions of consumer equilibrium: Necessary or First Order Condition and Supplementary or Second Order Condition.

To understand how the consumer reaches his equilibrium using the ordinal approach we need to understand the following terms:

• Indifference curve: The indifference curve shows the different combinations of two substitutes (goods) that yield the same level of satisfaction (utility) to the consumer. This means that the consumer is indifferent towards the consumption of two goods which are closely related to each other.
• Indifference Map: The indifference map contains different indifference curves showing the combinations of different quantities of two substitute goods on the basis of the consumer preferences. The consumer can make different combinations of goods by consuming less of one commodity or the other in such a way that all the combinations yield the same level of satisfaction.
• Marginal Rate of Substitution (MRS): The marginal rate of substitution defines the rate at which one commodity is substituted for another in such a way that the total utility (satisfaction) remains the same.
• Budget Line: As per the properties of the indifference curve, higher the indifference curve on the indifference map, the higher is the utility derived from the consumption. Thus, the consumer tries to reach to the highest possible indifference curve with two strong constraints: limited income and market price of goods and services.Since the amount of income in hand decides how high consumer can reach on his indifference map acts as a budgetary constraint. Therefore, the budget line represents the different quantity combinations of available commodities that a consumer can purchase given his level of income and the market price of goods and services.

Now, let’s understand how consumer reaches his equilibrium using the ordinal utility approach:

Necessary Condition or First Order Condition: Under the first order condition, the consumer reaches his equilibrium in the same manner as he does under the cardinal approach of the two-commodity model. It is expressed as:

By implication,
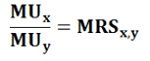Thus, the necessary condition of the cardinal approach to consumer equilibrium can be written as:

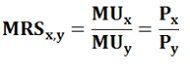Supplementary or Second Order Condition: The first order condition is necessary but not sufficient. Thus, the second order or supplementary condition requires that the necessary condition must be accomplished at the highest possible indifference curve on the indifference map.

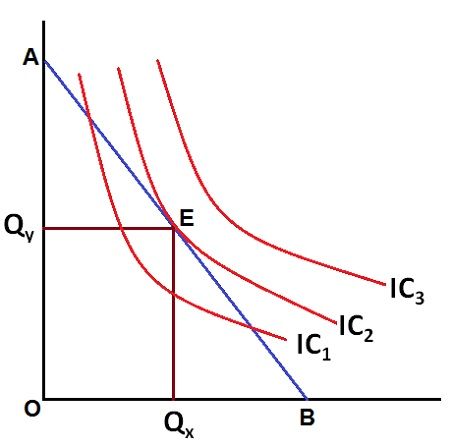
In the figure above, there are three indifference curves, Viz. IC₁, IC₂, and IC₃ presenting a hypothetical indifference map of the consumer. AB is the hypothetical budget line. At point ‘E’, the indifference curve IC₂ and Budget line AB intersect and hence, therefore, the slope of IC₂ = AB. At this point, both the necessary condition and the supplementary condition get fulfilled, and hence, the consumer attains equilibrium at point ‘E’.

We know that between any two points on the indifference curve:
ΔY. MU_y = ΔX. MU_x

Thus, the slope of the indifference curve can be written as:

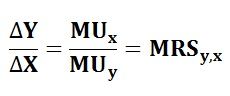The slope of budget line is given as:

In the figure above, at point ‘E’, MRS _{x, y} = P_x /P_y and hence the consumer is said to have attained equilibrium at this point. The IC₂ is tangent with the budget line AB, which shows that the consumer has reached to the highest possible indifference curve for a given level of his income and the market price of goods and services. Thus, at point ‘E’ consumer consumes quantity OQ_x of X and OQ_y of Y, which yields him the maximum utility or satisfaction.