Definition: The Marginal Rate of Substitution refers to the rate at which the consumer substitutes one commodity for another in such a way that the total utility (satisfaction) remains the same.
In other words, the marginal rate of substitution between two commodities, let’s say X and Y can be defined as the quantity of X required to replace one unit of Y or quantity of Y required to replace one unit of X in such a combination that the total utility remains unchanged. Hence, it is implied that the utility of units foregone or given up is equal to the utility of additional units of the commodity added to the combination.
The ordinal theory posits that the marginal rate of substitution (MRS) decreases. This means that as the consumer goes on substituting one commodity for another, the quantity of the commodity that a consumer sacrifice for an additional unit of another goes on decreasing. This can be illustrated by a table given below:
| Indifference Points | Combinations Y+X | Change in Y (-ΔY) | Change in X (ΔX) | Marginal Rate of Substitution y,x (ΔY/ ΔX) |
|---|---|---|---|---|
| P | 20+3 | - | - | - |
| Q | 15+5 | -10 | 2 | -5 |
| R | 8+10 | -7 | 5 | -1.4 |
| S | 3+17 | -5 | 7 | -0.71 |
| T | 1+25 | -2 | 8 | -0.25 |
As per the table, when the consumer moves from point P to Q on the indifference curve he gives up 10 units of commodity Y and gets only 2 units of commodity X, so that
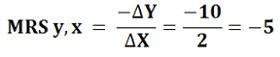As he moves down from point Q to R he further loses 7 units of Y and gets 5 units of X, giving
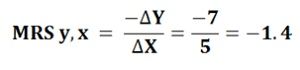Thus, as the consumer moves from point P to Q and from point Q to R the MRS decreases from -5 to -1.4. As the consumer moves further, the MRS goes on decreasing. This decreasing MRS causes the indifference curve to be convex to the origin.
Leave a Reply