Financial Market

Definition: Financial Market refers to a marketplace, where creation and trading of financial assets, such as shares, debentures, bonds, derivatives, currencies, etc. take place. It plays a crucial role in allocating limited resources, in the country’s economy. It acts as an intermediary between the savers and investors by mobilising funds between them.

The financial market provides a platform to the buyers and sellers, to meet, for trading assets at a price determined by the demand and supply forces.

Functions of Financial Market

The functions of the financial market are explained with the help of points below:

• It facilitates mobilisation of savings and puts it to the most productive uses.
• It helps in determining the price of the securities. The frequent interaction between investors helps in fixing the price of securities, on the basis of their demand and supply in the market.
• It provides liquidity to tradable assets, by facilitating the exchange, as the investors can readily sell their securities and convert assets into cash.
• It saves the time, money and efforts of the parties, as they don’t have to waste resources to find probable buyers or sellers of securities. Further, it reduces cost by providing valuable information, regarding the securities traded in the financial market.

The financial market may or may not have a physical location, i.e. the exchange of asset between the parties can also take place over the internet or phone also.

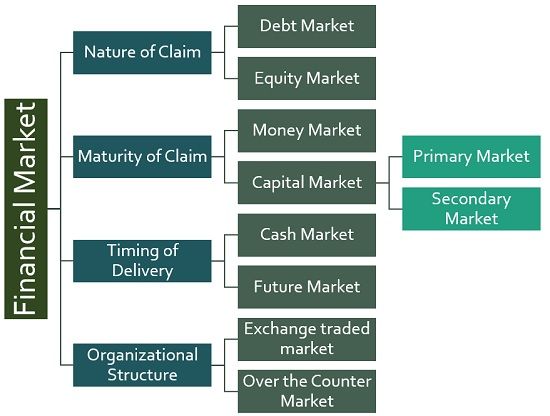
Classification of Financial Market

1. By Nature of Claim
   • Debt Market: The market where fixed claims or debt instruments, such as debentures or bonds are bought and sold between investors.
   • Equity Market: Equity market is a market wherein the investors deal in equity instruments. It is the market for residual claims.
2. By Maturity of Claim
   • Money Market: The market where monetary assets such as commercial paper, certificate of deposits, treasury bills, etc. which mature within a year, are traded is called money market. It is the market for short-term funds. No such market exist physically; the transactions are performed over a virtual network, i.e. fax, internet or phone.
   • Capital Market: The market where medium and long term financial assets are traded in the capital market. It is divided into two types:
     • Primary Market: A financial market, wherein the company listed on an exchange, for the first time, issues new security or already listed company brings the fresh issue.
     • Secondary Market: Alternately known as the Stock market, a secondary market is an organised marketplace, wherein already issued securities are traded between investors, such as individuals, merchant bankers, stockbrokers and mutual funds.
3. By Timing of Delivery
   • Cash Market: The market where the transaction between buyers and sellers are settled in real-time.
   • Futures Market: Futures market is one where the delivery or settlement of commodities takes place at a future specified date.
4. By Organizational Structure
   • Exchange-Traded Market: A financial market, which has a centralised organisation with the standardised procedure.
   • Over-the-Counter Market: An OTC is characterised by a decentralised organisation, having customised procedures.

Since last few years, the role of the financial market has taken a drastic change, due to a number of factors such as low cost of transactions, high liquidity, investor protection, transparency in pricing information, adequate legal procedures for settling disputes, etc.