Definition: The Regression Equation is the algebraic expression of the regression lines. It is used to predict the values of the dependent variable from the given values of independent variables.
If we take two regression lines, say Y on X and X on Y, then there will be two regression equations:
- Regression Equation of Y on X: This is used to describe the variations in the value Y from the given changes in the values of X. It can be expressed as follows:
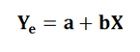
Where Ye is the dependent variable, X is the independent variable, and a & b are the two unknown constants that determine the position of the line. The parameter “a” tells about the level of the fitted line, i.e. the distance of a line above or below the origin and parameter “b” tells about the slope of the line, i.e. the change in the value of Y for one unit of change in X.The values of ‘a’ and ‘b’ can be obtained by a method of least squares. According to which the line should be drawn connecting all the plotted points in such a manner that the sum of the squares of the vertical deviations of actual Y from the estimated values of Y is the least, or a best-fitted line is obtained when ∑ (Y-Ye)2 is the minimum.
The following algebraic equations can be solved simultaneously to obtain the values of parameter ‘a’ and ‘b’.
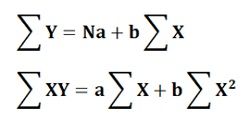
- Regression Equation of X on Y: This is used to describe the variations in Y from the given changes in the value of X. It can be expressed as follows:
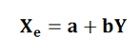
Where Xe is the dependent variable and Y is the independent variable. The parameters ‘a’ and ‘b’ are the two unknown constants. Again, ‘a’ tells about the level of fitted line and ‘b’ tells about the slope, i.e. the change in the value of X for a unit change in the value of Y.The following are the two normal equations that can be solved simultaneously to obtain the values of both the parameters ‘a’ and ‘b’.
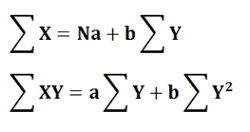
Note: The line can be completely determined only if the values of the constant parameters ‘a’ and ‘b’ are obtained.

Leave a Reply