Definition: The Regression Coefficient is the constant ‘b’ in the regression equation that tells about the change in the value of dependent variable corresponding to the unit change in the independent variable.
If there are two regression equations, then there will be two regression coefficients:
- Regression Coefficient of X on Y: The regression coefficient of X on Y is represented by the symbol bxy that measures the change in X for the unit change in Y. Symbolically, it can be represented as:
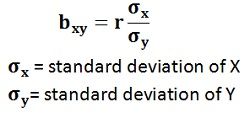 The bxy can be obtained by using the following formula when the deviations are taken from the actual means of X and Y:
The bxy can be obtained by using the following formula when the deviations are taken from the actual means of X and Y: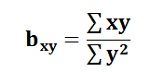 When the deviations are obtained from the assumed mean, the following formula is used:
When the deviations are obtained from the assumed mean, the following formula is used: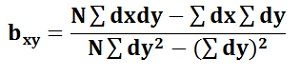
- Regression Coefficient of Y on X: The symbol byx is used that measures the change in Y corresponding to the unit change in X. Symbolically, it can be represented as:
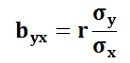
In case, the deviations are taken from the actual means; the following formula is used: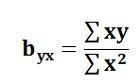
The byx can be calculated by using the following formula when the deviations are taken from the assumed means: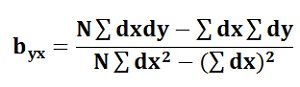
The Regression Coefficient is also called as a slope coefficient because it determines the slope of the line i.e. the change in the independent variable for the unit change in the independent variable.

Payal says
It is very amazing 😍
Zakiur says
thanks