Properties of Regression Coefficient

Definition: The constant ‘b’ in the regression equation (Y_e = a + bX) is called as the Regression Coefficient. It determines the slope of the line, i.e. the change in the value of Y corresponding to the unit change in X and therefore, it is also called as a “Slope Coefficient.”

Properties of Regression Coefficient

1. The correlation coefficient is the geometric mean of two regression coefficients. Symbolically, it can be expressed as:
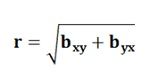
2. The value of the coefficient of correlation cannot exceed unity i.e. 1. Therefore, if one of the regression coefficients is greater than unity, the other must be less than unity.
3. The sign of both the regression coefficients will be same, i.e. they will be either positive or negative. Thus, it is not possible that one regression coefficient is negative while the other is positive.
4. The coefficient of correlation will have the same sign as that of the regression coefficients, such as if the regression coefficients have a positive sign, then “r” will be positive and vice-versa.
5. The average value of the two regression coefficients will be greater than the value of the correlation. Symbolically, it can be represented as
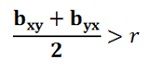
6. The regression coefficients are independent of the change of origin, but not of the scale. By origin, we mean that there will be no effect on the regression coefficients if any constant is subtracted from the value of X and Y. By scale, we mean that if the value of X and Y is either multiplied or divided by some constant, then the regression coefficients will also change.

Thus, all these properties should be kept in mind while solving for the regression coefficients.