North-West Corner Rule

Definition: The North-West Corner Rule is a method adopted to compute the initial feasible solution of the transportation problem. The name North-west corner is given to this method because the basic variables are selected from the extreme left corner.

The concept of North-West Corner can be well understood through a transportation problem given below:

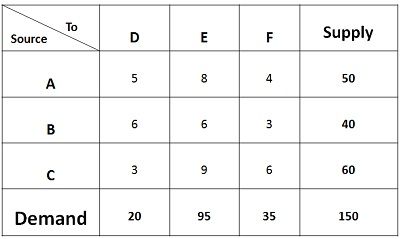
In the table, three sources A, B and C with the production capacity of 50 units, 40 units, 60 units of product respectively is given. Every day the demand of three retailers D, E, F is to be furnished with at least 20 units, 95 units and 35 units of product respectively. The transportation costs are also given in the matrix.

The prerequisite condition for solving the transportation problem is that demand should be equal to the supply. In case the demand is more than supply, then dummy origin is added to the table. The supply of dummy origin will be equal to the difference between the total supply and total demand. The cost associated with the dummy origin will be zero.

Similarly, in case the supply is more than the demand, then dummy source is created whose demand will be equivalent to the difference between supply and demand. Again the cost associated with the dummy source will be zero.

Once the demand and supply are equal, the following procedure is followed:

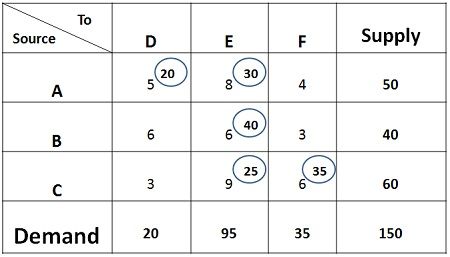
1. Select the north-west or extreme left corner of the matrix, assign as many units as possible to cell AD, within the supply and demand constraints. Such as 20 units are assigned to the first cell, that satisfies the demand of destination D while the supply is in surplus.
2. Now move horizontally and assign 30 units to the cell AE. Since 30 units are available with the source A, the supply gets fully saturated.
3. Now move vertically in the matrix and assign 40 units to Cell BE. The supply of source B also gets fully saturated.
4. Again move vertically, and assign 25 units to cell CE, the demand of destination E is fulfilled.
5. Move horizontally in the matrix and assign 35 units to cell CF, both the demand and supply of origin and destination gets saturated. Now the total cost can be computed.

The Total cost can be computed by multiplying the units assigned to each cell with the concerned transportation cost. Therefore,

Total Cost = 20*5+ 30*8+ 40*6+ 25*9+ 35*6 = Rs 1015