Definition: The Sample is the representative of the population from where it is drawn, and thus the Sample Distribution measures the frequency with which the number of subjects that make up the sample is actually drawn for a given research study.
The samples are drawn when the population size is large, and it is not possible for an investigator to completely enumerate all the items of the population. Generally, the selection of the samples from the population is restricted to the simple random sampling, wherein all the items have equally and the likely chance of being selected in the sample. Thus, the sample is the subset of the population that reflects the characteristics or attributes of the population.
For example, if the sample of 500 students is selected from the population of 20,000 students of a particular college, then on the basis of this information the value of the sample mean and standard deviation can be computed. These are symbolized as:
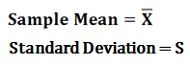These measures (mean and standard deviation) characterizing the sample are called as the statistics.
Note: It is to be noted that several sample distributions are possible from a given set of population.
Leave a Reply