Definition: The Sampling Distribution of the Mean is the mean of the population from where the items are sampled. If the population distribution is normal, then the sampling distribution of the mean is likely to be normal for the samples of all sizes.
Following are the main properties of the sampling distribution of the mean:
- Its mean is equal to the population mean, thus,
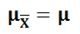 (?X͞ =sample mean and ?p Population mean)
(?X͞ =sample mean and ?p Population mean) - The population standard deviation divided by the square root of the sample size is equal to the standard deviation of the sampling distribution of the mean, thus:
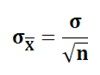 (σ = population standard deviation, n = sample size)
(σ = population standard deviation, n = sample size) - The sampling distribution of the mean is normally distributed. This means, the distribution of sample means for a large sample size is normally distributed irrespective of the shape of the universe, but provided the population standard deviation (σ) is finite. Generally, the sample size 30 or more is considered large for the statistical purposes. If the population is normal, then the distribution of sample means will be normal, irrespective of the sample size.
σ͞x is a measure of precision through which the sample mean can be used to estimate the true value of a population mean. ?σ͞x varies in direct proportion to the change in the original population and inversely to the square of sample size ‘n’. Thus, the greater the variations in the original items of the population greater the variation expected in sampling error in using ͞x as an estimate of ?. It is to be noted that larger the sample size smaller is the standard error and vice-versa.

Leave a Reply