Definition: The Sampling Distribution helps in determining the degree to which the sample means from different samples differ from each other, and the population mean to determine the degree of closeness between the particular sample mean to the population mean.
In other words, the sampling distribution constitutes the theoretical basis of inferential statistics that involves determining the extent to which the sample statistic vary from each other and the population parameter. Here, the sample statistic is the sample mean, and the population parameter is the population means.
Here the sample mean is symbolized as ? and the standard deviation of the sampling distribution of the mean is called as a standard error of mean and is symbolized as 
The standard error of mean is the most common method used to measure the extent to which the sample means vary from each other. The formula used to calculate the standard error of mean is: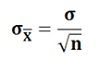
Note: This formula can be used when the samples are drawn from the finite population with replacement or when the population size is infinite.
If the sample means are closer to the population mean, then the value of the standard error of mean will be small and if there are considerable variations in the sample means then the standard error of mean will be large.
Thus, the importance of sampling distribution lies in the fact that it helps in determining the sampling errors and their magnitude in terms of standard error. It is generally observed that the fluctuations in the sample mean are more than the fluctuations in the actual population when the sampling is done with replacement.
Leave a Reply