Definition: The Sampling Distribution of Proportion measures the proportion of success, i.e. a chance of occurrence of certain events, by dividing the number of successes i.e. chances by the sample size ’n’. Thus, the sample proportion is defined as p = x/n.
The sampling distribution of proportion obeys the binomial probability law if the random sample of ‘n’ is obtained with replacement. Such as, if the population is infinite and the probability of occurrence of an event is ‘π’, then the probability of non-occurrence of the event is (1-π). Now consider all the possible sample size ‘n’ drawn from the population and estimate the proportion ‘p’ of success for each. Then the mean (?p) and the standard deviation (σp) of the sampling distribution of proportion can be obtained as:

?p = mean of proportion
π = population proportion which is defined as π = X/N, where X is the number of elements that possess a certain characteristic and N is the total number of items in the population.
σp = standard error of proportion that measures the success (chance) variations of sample proportions from sample to sample
n= sample size, If the sample size is large (n≥30), then the sampling distribution of proportion is likely to be normally distributed.
The following formula is used when population is finite, and the sampling is made without the replacement:

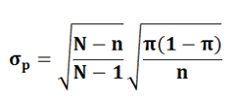
Leave a Reply