Definition: The Sampling Distribution of the Difference between Two Means shows the distribution of means of two samples drawn from the two independent populations, such that the difference between the population means can possibly be evaluated by the difference between the sample means.
Let say, there are two populations, first of size N1, with mean ?1, and standard deviation σ1 and the second of size N2, with mean ?2, and standard deviation σ2. The two independent random samples are drawn, one from the population of size N1 and the other from the population of size N2. Suppose X͞1 and X͞2 are the two sample means, then we can estimate the possible difference between the population means, Viz. ?1 -?2 by the difference of sample means X͞1 – X͞2.
The following are the main properties of the sampling distribution of the difference between two means (X͞1 – X͞2):
- When the samples are selected randomly from the two independent populations, then the mean of the sampling distribution of the difference between the two means, i.e. X͞1 – X͞2, denoted by? X͞1 – X͞2 is equal to the difference between the Population Means. Symbolically,
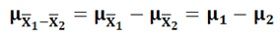
- The standard deviation of sampling distribution of differences between two means, i.e. X͞1 – X͞2 is also called as the standard error of X͞1 – X͞2 and is denoted by:
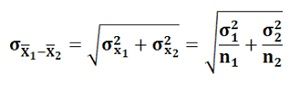
Since, X͞1 and X͞2 are the independent random variables, so the variance of their difference is equal to the sum of their variance. - If X͞1 and X͞2 are the means of two samples drawn from two large and independent populations the sampling distribution of the difference between two means will be normal.
Note: It is to be noted that when the sampling is done without the replacement, and the population is finite, then the following formula is used to calculate the standard error:

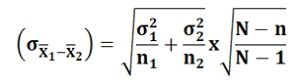
Leave a Reply