Definition: The t-distribution is a probability distribution method wherein the hypothesis of the mean of a small sample is tested, which is drawn from the systematic population whose standard deviation is unknown. It is a statistical measure used to compare the observed data with the data expected to be obtained from a specific hypothesis.
Applications of t-distribution
The following are the important applications of the t-distribution:
- Test of Hypothesis of the Population Mean: (Sample size ‘n’ is small). When the population is normally distributed, and the standard deviation ‘σ’ is unknown, then “t” statistic is calculated as:
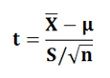 Where,
Where,
X͞ = Sample Mean
? = Population Mean
n = Sample size
S = Standard deviation of the sample calculated by applying the following formula: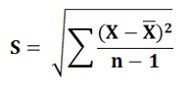 The null hypothesis is tested to check whether there is a significant difference between the X͞ and ?. If the calculated value of ‘t’ exceeds the table value of ‘t’ at a specific significance level, then the null hypothesis is rejected considering the difference between the X͞ and ? as significant.On the other hand, if the calculated value of ‘t’ is less than the table value of ‘t’, then the null hypothesis is accepted. It is to be noted that this test is based on the degrees of freedom, i.e. n-1.
The null hypothesis is tested to check whether there is a significant difference between the X͞ and ?. If the calculated value of ‘t’ exceeds the table value of ‘t’ at a specific significance level, then the null hypothesis is rejected considering the difference between the X͞ and ? as significant.On the other hand, if the calculated value of ‘t’ is less than the table value of ‘t’, then the null hypothesis is accepted. It is to be noted that this test is based on the degrees of freedom, i.e. n-1. - Test of Hypothesis of the Difference Between Two Means: In Testing hypothesis about the difference between two means drawn from the two systematic population whose variance is unknown, then t-test can be calculated in two ways:
Variances are equal: When the population variances, though unknown are taken as equal, then the t- statistic to be used is:
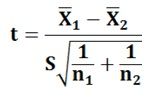 Where,
Where,
X͞1 and X͞2 are the sample means of sample 1 of size n1 and sample 2 of size n2.S is the common standard deviation obtained by pooling the data from both the samples and can be calculated by applying the following formula:
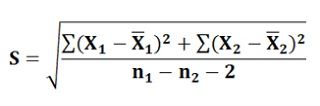 The null hypothesis is that there is no difference between two means and’ is accepted when the calculated value of ‘t’ at a specified significance level is less than the table value of ‘t’ and is rejected when the calculated value exceeds the table value.
The null hypothesis is that there is no difference between two means and’ is accepted when the calculated value of ‘t’ at a specified significance level is less than the table value of ‘t’ and is rejected when the calculated value exceeds the table value.Variances are Unequal: When the population variances are not equal, then we use the unbiased estimators S12 and S22. In this case, the sampling has the huge variability than the population variability and statistic to be used is:
?1 and ?2 are the two population means.
This statistic may not strictly follow t-distributions, but however it can be approximated by t-distribution with the modified value for the degrees of freedom given by:
- Test of Hypothesis of the Difference Between Two Means With Dependent Samples: In several situations, it is possible that the samples are drawn from the two populations that are dependent on each other. Thus, the samples are said to be dependent, as each observation included in sample one is associated with the particular observation in the second sample. Hence, due to this property the t-test that will be used here is called the paired t-test.
This test is applied in the situations when before and after experiments are to be compared. Usually, two methods are adopted that are related to each other. The following statistic is used when the means of both the methods applied is equal i.e. ?1 = ?2
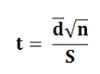 This statistic follows t- distribution with (n-1) degrees of freedom, where d͞ = mean of the differences calculated as:
This statistic follows t- distribution with (n-1) degrees of freedom, where d͞ = mean of the differences calculated as: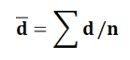
S is the standard deviation of differences and is calculated by applying the following formula: - Test of Hypothesis about the Coefficient of Correlation: There are three cases of testing the hypothesis about the coefficient of correlation. These are:
Case -1: When the population coefficient of correlation is zero, i.e. ρ = 0. The coefficient of correlation measures the degree of relationship between the variables, and when ρ = 0, then there is no statistical relationship between the variables. To test the null hypothesis which assumes that there is no correlation between the population, it is necessary that the sample coefficient of correlation ‘r’ is known. The test statistic to be used is: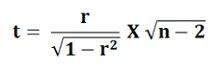 Case -2: When the Population Coefficient of Correlation is equal to some other value, other than zero, i.e. ρ≠0. In this case, the test based on t-distribution will not be correct and hence the hypothesis is tested using the Fisher’s z- transformation. Here the ‘r’ is transformed into ‘z’ by:
Case -2: When the Population Coefficient of Correlation is equal to some other value, other than zero, i.e. ρ≠0. In this case, the test based on t-distribution will not be correct and hence the hypothesis is tested using the Fisher’s z- transformation. Here the ‘r’ is transformed into ‘z’ by: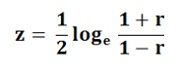 Here, loge is a natural logarithm. The common logarithm can be shifted to a natural algorithm by multiplying it by the factor 2.3026. Thus,loge X = 2.3026 log 10 X, where X is the positive integerSince, ½ X (2.3026) = 1.1513, then the following transformation formula is used:
Here, loge is a natural logarithm. The common logarithm can be shifted to a natural algorithm by multiplying it by the factor 2.3026. Thus,loge X = 2.3026 log 10 X, where X is the positive integerSince, ½ X (2.3026) = 1.1513, then the following transformation formula is used: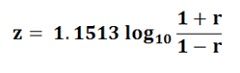 The following statistic is used to test the null hypotheses:
The following statistic is used to test the null hypotheses: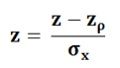 This follows the normal distribution and the test is said to be more appropriate as long as the sample size is large.
This follows the normal distribution and the test is said to be more appropriate as long as the sample size is large.Case-3: When the hypothesis is tested for the difference between two Independent Correlation Coefficients: To test the hypothesis of two correlations derived from the two separate samples, then the difference of the two corresponding values of z is to be compared with the standard error of the difference. The following statistic is used:

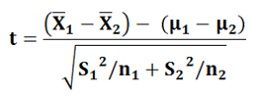
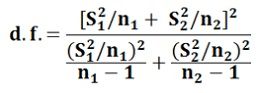
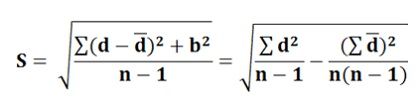
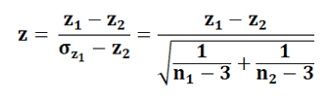
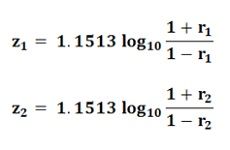
Leave a Reply