Chi-Square Distribution

Definition: The Chi-Square Distribution, denoted as χ² is related to the standard normal distribution such as, if the independent normal variable, let’s say Z assumes the standard normal distribution, then the square of this normal variable Z² has the chi-square distribution with ‘K’ degrees of freedom. Here, K is the sum of the independent squared normal variables.

The Sampling distribution of chi-square can be closely approximated by a continuous normal curve as long as the sample size remains large. The probability function of Chi-square can be given as:
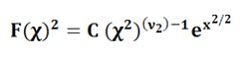Where,
e = 2.71828
ν= number of degrees of freedom
C = constant depending on ν

Through this, it is clear that the chi-square has only one parameter, i.e. degrees of freedom.

Properties of Chi-Square Distribution

 

1. The chi-square distribution is a continuous probability distribution with the values ranging from 0 to ∞ (infinity) in the positive direction. The χ2 can never assume negative values.
2. The shape of the chi-square distribution depends on the number of degrees of freedom ‘ν’. When ‘ν’ is small, the shape of the curve tends to be skewed to the right, and as the ‘ν’ gets larger, the shape becomes more symmetrical and can be approximated by the normal distribution.
3. The mean of the chi-square distribution is equal to the degrees of freedom, i.e. E(χ²) = ‘ν’. While the variance is twice the degrees of freedom, Viz. n(χ²) = 2ν.
4. The χ2 distribution approaches the normal distribution as ν gets larger with mean ν and standard deviation as √2χ². It has been determined that quantity √2χ² gives a better approximation to normality than the χ²  itself if the values are about 30 or more. Thus, the mean and standard deviation of the distribution of √2χ²  is equal to √2ν-1 and one respectively.
5. The sum of independent χ² is itself a χ²  variate. Suppose, χ₁² is a χ²  variate with degrees of freedom ν₁ and χ₂² is another χ² variate with degrees of freedom ν₂, then their sum χ₁² + χ₂² will be equal to χ² variate with ν₁+ ν₂ degrees of freedom. This property is called as the additive property of Chi-square.

Thus, χ² distribution depends on the degrees of distribution as its shape changes with the change in the ‘ν’, and as ‘ν’ becomes greater, χ²  gets approximated by the normal distribution.