F-Distribution

Definition: The F-Distribution is also called as Variance Ratio Distribution as it usually defines the ratio of the variances of the two normally distributed populations. The F-distribution got its name after the name of R.A. Fisher, who studied this test for the first time in 1924.

Symbolically, the quantity is distributed as F-distribution with ν₁ =n₁-1 and ν₂ = n₂-1 degrees of freedom and is represented as:

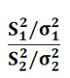Where,
S₁² is the unbiased estimator of σ₁² and is calculated as:

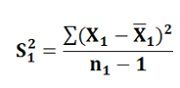S₂² is the unbiased estimator of σ₂² and is calculated as:

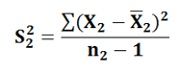The parameters of the F-distribution are degrees of freedom ν₁ for the numerator and degrees of freedom ν₂ for the denominator. Thus, with the change in the values of these parameters the distribution also changes. The F distribution probability density function is given by:

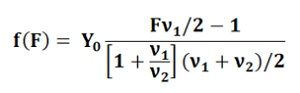Y₀ = constant depending on the values of ν₁ and ν₂.

For testing the hypothesis of the equality of two population variances, the following statistic is used:

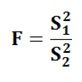Here, the Null hypothesis = σ₁² = σ₂² which follows the F-distribution with degrees of freedom ν₁ and ν₂. Often, the larger sample variance is placed in the numerator for the convenient computations. In doing so, we get the ratio of sample variance equals to or greater than one.

If the computed value of F exceeds the table value of F, then the null hypothesis is rejected and the alternative hypothesis gets accepted. On the other hand, if the computed value of F is less than the table value, the null hypothesis is accepted.