Properties of F-Distribution

Definition: The F-distribution depends on the degrees of freedom and is usually defined as the ratio of variances of two populations normally distributed and therefore it is also called as Variance Ratio Distribution.

Properties of F-Distribution

There are several properties of F-distribution which are explained below:

1. The F-distribution is positively skewed and with the increase in the degrees of freedom ν₁ and ν₂, its skewness decreases.
2. The value of the F-distribution is always positive, or zero since the variances are the square of the deviations and hence cannot assume negative values. Its value lies between 0 and ∞.
3. The statistic used to calculate the value of mean and variance is:
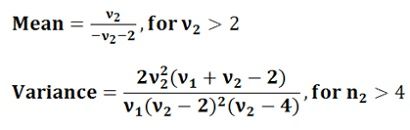
4. The shape of the F-distribution depends on its parameters ν₁ and ν₂ degrees of freedom.
5. The values of the area lying on the left-hand side of the distribution can be found out by taking the reciprocal of F values corresponding to the right-hand side and the degrees of freedom in the numerator and the denominator are interchanged. This is called as Reciprocal Property of F-distribution. Symbolically, it can be represented as: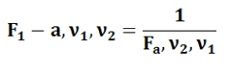This property is mainly used in the situations when the values of the lower tail F values are to be determined corresponding to the upper tail F values.

Thus, these are the properties of F-distribution that tells how the sample is distributed under study and what statistical inferences can be drawn therefrom.