Definition: The Linear Homogeneous Production Function implies that with the proportionate change in all the factors of production, the output also increases in the same proportion. Such as, if the input factors are doubled the output also gets doubled. This is also known as constant returns to a scale.
The production function is said to be homogeneous when the elasticity of substitution is equal to one. The linear homogeneous production function can be used in the empirical studies because it can be handled wisely. That is why it is widely used in linear programming and input-output analysis. This production function can be shown symbolically:
nP = f(nK, nL)
Where, n = number of times
nP = number of times the output is increased
nK= number of times the capital is increased
nL = number of times the labor is increased
Thus, with the increase in labor and capital by “n” times the output also increases in the same proportion. The concept of linear homogeneous production function can be further comprehended through the illustration given below:
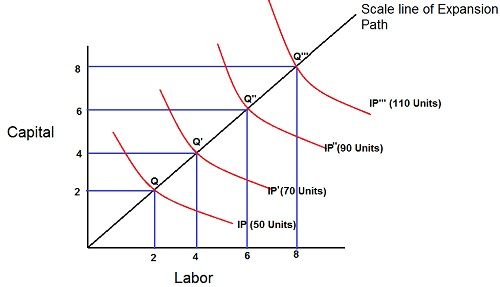 In the case of a linear homogeneous production function, the expansion is always a straight line through the origin, as shown in the figure. This means that the proportions between the factors used will always be the same irrespective of the output levels, provided the factor prices remains constant.
In the case of a linear homogeneous production function, the expansion is always a straight line through the origin, as shown in the figure. This means that the proportions between the factors used will always be the same irrespective of the output levels, provided the factor prices remains constant.

Akanksha says
Thank you so much for such a lucid explanation ..
Can you also explain the expansion path of the linear homogeneous production function