Definition: The Spearman’s Rank Correlation Coefficient is the non-parametric statistical measure used to study the strength of association between the two ranked variables. This method is applied to the ordinal set of numbers, which can be arranged in order, i.e. one after the other so that ranks can be given to each.
In the rank correlation coefficient method, the ranks are given to each individual on the basis of its quality or quantity, such as ranking starts from position 1st and goes till Nth position for the one ranked last in the group.
The formula to calculate the rank correlation coefficient is:
Where, R = Rank coefficient of correlation
D = Difference of ranks
N = Number of Observations
The value of R lies between ±1 such as:
R =+1, there is a complete agreement in the order of ranks and move in the same direction.
R=-1, there is a complete agreement in the order of ranks, but are in opposite directions.
R =0, there is no association in the ranks.
While solving for the rank correlation coefficient one may come across the following problems:
- Where actual Ranks are given
- Where ranks are not given
- Equal Ranks or Tie in Ranks
Where actual ranks are given: An individual must follow the following steps to calculate the correlation coefficient:
- First, the difference between the ranks (R1-R2) must be calculated, denoted by D.
- Then, square these differences to remove the negative sign and obtain its sum ∑D2.
- Apply the formula as shown above.
Where ranks are not given: In case the ranks are not given, then the individual may assign the rank by taking either the highest value or the lowest value as 1. Whatever criteria is being decided the same method should be applied to all the variables.
Equal Ranks or Tie in Ranks: In case the same ranks are assigned to two or more entities, then the ranks are assigned on an average basis. Such as if two individuals are ranked equal at third position, then the ranks shall be calculated as:
(3+4)/2 = 3.5
The formula to calculate the rank correlation coefficient when there is a tie in the ranks is:
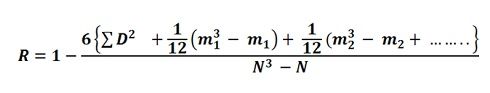 Where m = number of items whose ranks are common.
Where m = number of items whose ranks are common.
Note: The Spearman’s rank correlation coefficient method is applied only when the initial data are in the form of ranks, and N (number of observations) is fairly small, i.e. not greater than 25 or 30.

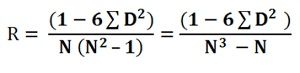
Shubham Dubey says
It’s good and pretty easy to understand.
Jackline Adhiambo says
Nice formula