Definition: The Central Limit Theorem states that when a large number of simple random samples are selected from the population and the mean is calculated for each then the distribution of these sample means will assume the normal probability distribution.
In other words, the sample means will be normally distributed when the mean and standard deviation of the population is given, and large random samples are selected from the population, irrespective of whether the population is normal or skewed. Symbolically the central limit theorem can be explained as:
When ‘n’ number of independent random variables are given each having the same distribution, then:
X = X1+X2+X3+X4+…. +Xn, the mean and variance of X will be:
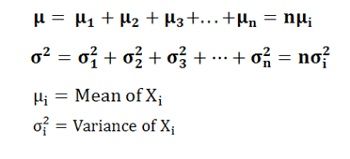The following three probability distributions must be understood for the complete understanding of the Sampling Theory:
The utility of the central limit theorem is that it requires no condition on distribution patterns of the random variables and in fact, uses the practical method to compute the approximate probability values for the arbitrarily distributed random variables.
Also, it helps to determine why the vast number of phenomena shows approximate normal distribution. Suppose, the population is skewed, the skewness of the sampling distribution is inversely proportional to the square root of the sample size. Thus, if the sample size is 25, then the sampling distribution exhibits only one-fifth as much skewness as the population.
Thus, it can be said that the sampling distribution of the sample mean assumes the normal distribution irrespective of what distribution a population assumes from which the samples are drawn, and the approximation to the normal distribution is likely to increase with the increase in the sample size.
Leave a Reply